How to Draw a Circle in Computer Graphics
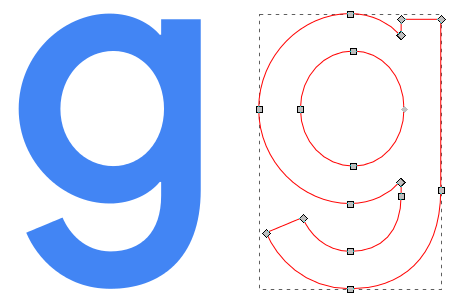
A fundamental operation in computer graphics is to describe lines and circles. For instance, these are used equally the components of scalable fonts and vector graphics; the letter "one thousand" is specified as a series of lines and curves, then that when yous zoom in on information technology the computer can redraw it at any resolution is needed. If the organisation but stored the pixels for the letter shape, then zooming in would event in a low quality paradigm.
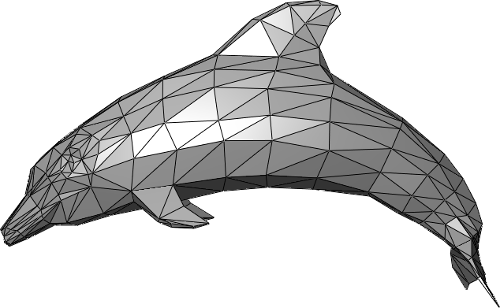
In 3D graphics shapes are often stored using lines and curves that mark out the edges of tiny flat surfaces (ordinarily triangles), each of which is so small that you can't see them unless you lot zoom right in.
The lines and circles that specify an object are unremarkably given using numbers (for case, a line betwixt a given starting and finishing position or a circle with a given centre and radius). From this a graphics program must calculate which pixels on the screen should be coloured in to represent the line or circle, or it may but need to piece of work out where the line is without drawing it.
For example, here'due south a filigree of pixels with 5 lines shown magnified. The vertical line would accept been specified as going from pixel (2, 9) to (2, 16) – that is, starting 2 across and 9 upward, and finishing 2 across and 16 up. Of course, this is only a pocket-size part of a screen, equally normally they are more than like 1000 past thou pixels or more; even a smartphone screen is hundreds of pixels high and wide.
These are things that are easy to exercise with pencil and newspaper using a ruler and compass, but on a computer the calculations need to be done for every pixel, and if y'all utilise the wrong method then it volition have also long and the image will be displayed slowly or a live animation volition appear jerky. In this section we will await into some very simple but clever algorithms that enable a computer to do these calculations very rapidly.
To draw a line, a computer must work out which pixels demand to be filled so that the line looks straight. Yous tin can endeavor this by colouring in squares on a grid, such as the 1 below (they are many times bigger than the pixels on a normal printer or screen). We'll place the pixels on the grid using ii values, (x, y), where ten is the distance across from the left, and y is the distance upward from the lesser. The bottom left pixel below is (0, 0), and the pinnacle right one is (nineteen, 19).
Try to depict these direct lines by clicking on pixels in the following grid:
- from (2, 17) to (10, 17)
- from (18, 2) to (18, 14)
- from (1, five) to (8, 12)
Cartoon a horizontal, vertical or 45 caste line similar the ones above is piece of cake; information technology'due south the ones at different angles that require some adding.
Without using a ruler, can you draw a directly line from A to B on the following grid by colouring in pixels?
Once you take finished drawing your line, try checking it with a ruler. Identify the ruler and so that it goes from the center of A to the centre of B. Does it cross all of the pixels that you have coloured?
The mathematical formula for a line is . This gives yous the y value for each 10 value beyond the screen, and you get to specify two things: the slope of the line, which is , and where the line crosses the y axis, which is . In other words, when yous are x pixels across the screen with your line, the pixel to color in would be (, ).
For example, choosing and means that the line would become through the points (0, 3), (1, five), (2, seven), (3, nine) and so on. This line goes up 2 pixels for every one across , and crosses the y centrality 3 pixels up ().
You should experiment with drawing graphs for various values of and (for instance, start with , and try these three lines: , and ) past putting in the values. What angle are these lines at?
The formula tin can be used to piece of work out which pixels should be coloured in for a line that goes between and . What are and for the points A and B on the grid below?
See if you can work out the and values for a line from A to B, or you can calculate them using the post-obit formulas:
Now depict the same line as in the previous section (between A and B) using the formula to summate for each value of from to (you will need to circular to the nearest integer to work out which pixel to colour in). If the formulas have been applied correctly, the value should range from to .
Once you have completed the line, bank check it with a ruler. How does it compare to your offset try?
At present consider the number of calculations that are needed to piece of work out each betoken. It won't seem like many, but remember that a computer might be calculating hundreds of points on thousands of lines in a complicated image. Although this formula works fine, it'south also slow to generate the complex graphics needed for skilful animations and games. In the next section we will explore a method that greatly speeds this up.
A faster mode for a computer to calculate which pixels to colour in is to use Bresenham's line algorithm. It follows these simple rules. Get-go, calculate these three values:
To depict the line, fill the starting pixel, and then for every position forth the x centrality:
- If is less than 0, draw the new pixel on the same line as the last pixel, and add to .
- If was 0 or greater, draw the new pixel one line higher than the last pixel, and add together to .
- Repeat this decision until we reach the terminate of the line.
Without using a ruler, employ Bresenham's line algorithm to draw a directly line from A to B:
In one case you take completed the line, check information technology with a ruler. How does it compare to the previous attempts?
So far the version of Bresenham's line drawing algorithm that yous have used only works for lines that have a gradient (slope) between 0 and 1 (that is, from horizontal to 45 degrees). To make this algorithm more than full general, and so that it can be used to describe any line, some additional rules are needed:
- If a line is sloping downward instead of sloping upward, so when P is 0 or greater, describe the next column'southward pixel i row below the previous pixel, instead of above it.
- If the change in value is greater than the change in value (which ways that the gradient is more 1), and then the calculations for A, B, and the initial value for P will demand to be inverse. When calculating A, B, and the initial P, apply Ten where you previously would take used Y, and vice versa. When drawing pixels, instead of going across every column in the X centrality, go through every row in the Y axis, cartoon one pixel per row.
In the filigree above, cull 2 points of your own that are unique to yous. Don't merely cull points that will give horizontal or vertical lines!
Now use Bresenham'southward algorithm to depict the line. Check that it gives the same points as you would have chosen using a ruler, or using the formula . How many arithmetic calculations (multiplications and additions) were needed for Bresenham'due south algorithm? How many would have been needed if you used the formula? Which is faster (conduct in mind that calculation is a lot faster than multiplying for most computers).
You could write a program or pattern a spreadsheet to do these calculations for you – that's what graphics programmers have to do.
Every bit well as straight lines, another common shape that computers oft need to draw are circles. An algorithm similar to Bresenham'due south line cartoon algorithm, called the Midpoint Circle Algorithm, has been developed for drawing a circle efficiently.
A circle is defined by a centre point, and a radius. Points on a circle are all the radius distance from the middle of the circle.
Effort to describe a circumvolve by mitt past filling in pixels (without using a ruler or compass). Annotation how hard information technology is to make the circumvolve look round.
It is possible to draw the circle using a formula based on Pythagoras' theorem, but it requires calculating a foursquare root for each pixel, which is very slow. The post-obit algorithm is much faster, and only involves simple arithmetic and so information technology runs apace on a reckoner.
Hither are the rules for the midpoint circumvolve algorithm for a circumvolve around (, ) with a radius of :
Repeat the following rules in order until becomes greater than :
- Fill the pixel at coordinate (, )
- Increase by
- Increase by 1
- If is greater than or equal to 0, subtract from , and and so subtract 1 from .
Follow the rules to draw a circle on the filigree, using (, ) every bit the centre of the circle, and the radius. Notice that it will but depict the first of the circle and and then it stops because is greater than !
When becomes greater than , one eighth (an octant) of the circle is drawn. The remainder of the circle tin exist fatigued by reflecting the octant that you already have (y'all can think of this as repeating the pattern of steps you but did in contrary). Y'all should reflect pixels along the X and Y axis, and then that the line of reflection crosses the middle of the eye pixel of the circle. Half of the circle is at present fatigued, the left and the right half. To add the residue of the circle, some other line of reflection must be used. Can y'all piece of work out which line of reflection is needed to consummate the circumvolve?
Quadrants and octants Jargon Buster
A quadrant is a quarter of an surface area; the four quadrants that encompass the whole area are marked off by a vertical and horizontal line that cantankerous. An octant is i 8th of an area, and the 8 octants are marked off by 4 lines that intersect at 1 indicate (vertical, horizontal, and 2 diagonal lines).
To complete the circle, you lot need to reverberate along the diagonal. The line of reflection should have a slope of 1 or -1, and should cross through the middle of the center pixel of the circle.
While using a line of reflection on the octant is easier for a human to understand, a computer can depict all of the reflected points at the aforementioned fourth dimension information technology draws a point in the start octant considering when it is drawing pixel with an offset of (10,y) from the middle of the circumvolve, it tin also draw the pixels with offsets (x, -y), (-x, y), (-10, -y), (y, x), (y, -x), (-y, 10) and (-y, -x), which give all 8 reflections of the original point!
Past the way, this kind of algorithm tin can be adjusted to draw ellipses, but it has to draw a whole quadrant because yous don't have octant symmetry in an ellipse.
Computers demand to draw lines, circles and ellipses for a wide multifariousness of tasks, from game graphics to lines in an builder'south cartoon, and even a tiny circle for the dot on the peak of the letter 'i' in a discussion processor. By combining line and circle drawing with techniques like 'filling' and 'antialiasing', computers tin can draw smooth, articulate images that are resolution independent. When an paradigm on a estimator is described as an outline with fill colours information technology is called vector graphics – these tin exist re-fatigued at any resolution. This means that with a vector image, zooming in to the image volition non crusade the pixelation seen when zooming in to bitmap graphics, which merely store the pixels and therefore make the pixels larger when you zoom in. Notwithstanding, with vector graphics the pixels are recalculated every time the image is redrawn, and that's why information technology's important to use a fast algorithm similar the ane to a higher place to draw the images.
Outline fonts are one of the most common uses for vector graphics as they permit the text size to be increased to very large sizes, with no loss of quality to the letter shapes.
Computer scientists accept institute fast algorithms for drawing other shapes too, which means that the epitome appears quickly, and graphics can display quickly on relatively boring hardware – for example, a smartphone needs to do these calculations all the fourth dimension to display images, and reducing the amount of calculations can extend its bombardment life, also as make it appear faster.
As usual, things aren't quite as simple as shown here. For instance, consider a horizontal line that goes from (0, 0) to (10, 0), which has 11 pixels. At present compare it with a 45 degree line that goes from (0, 0) to (10, 10). Information technology still has eleven pixels, but the line is longer (near 41% longer to be precise). This means that the line would appear thinner or fainter on a screen, and extra work needs to be done (mainly anti-aliasing) to brand the line look ok. We've but simply begun to explore how techniques in graphics are needed to quickly return high quality images.
Line and circle drawing Project
To compare Bresenham'south method with using the equation of a line (), choose your ain start and end point of a line (of class, make sure it's at an interesting bending), and show the calculations that would be made by each method. Count up the number of additions, subtractions, multiplications and divisions that are made in each case to make the comparing. Note that addition and subtraction is commonly a lot faster than multiplication and partition on a figurer.
You tin estimate how long each operation takes on your calculator by running a plan that does thousands of each functioning, and timing how long it takes for each. From this you can estimate the total time taken past each of the two methods. A good measurement for these is how many lines (of your chosen length) your computer could calculate per second.
If you're evaluating how fast circle drawing is, yous tin can compare the number of add-on and multiplication operations with those required past the Pythagoras formula that is a basis for the simple equation of a circle (for this calculation, the line from the eye of the circle to a particular pixel on the edge is the hypotenuse of a triangle, and the other two sides are a horizontal line from the centre, and a vertical line up to the point that we're wanting to locate. You'll need to calculate the y value for each 10 value; the length of the hypotenuse is always equal to the radius).
Source: https://www.csfieldguide.org.nz/en/chapters/computer-graphics/drawing-lines-and-circles/
0 Response to "How to Draw a Circle in Computer Graphics"
Post a Comment